Graphs and Occam’s Razor

One argument / point of criticism I often hear from people who start exploring Directed Acyclic Graphs (DAG) is that graphical models can quickly become very complex. When you read about the methodology for the first time you get walked through all these toy models – small, well-behaved examples with nice properties, in which causal inference works like a charm.

But then you go out to apply the methods to your own particular problem and you soon realize that it’s very hard to keep the model at a manageable size. Because how can you be sure that two variables aren’t related to each other? So you better keep a link between them. But suddenly everything depends on everything and all hope for getting at the desired P(y|do)) gets lost.

Indeed, in complete networks like this one

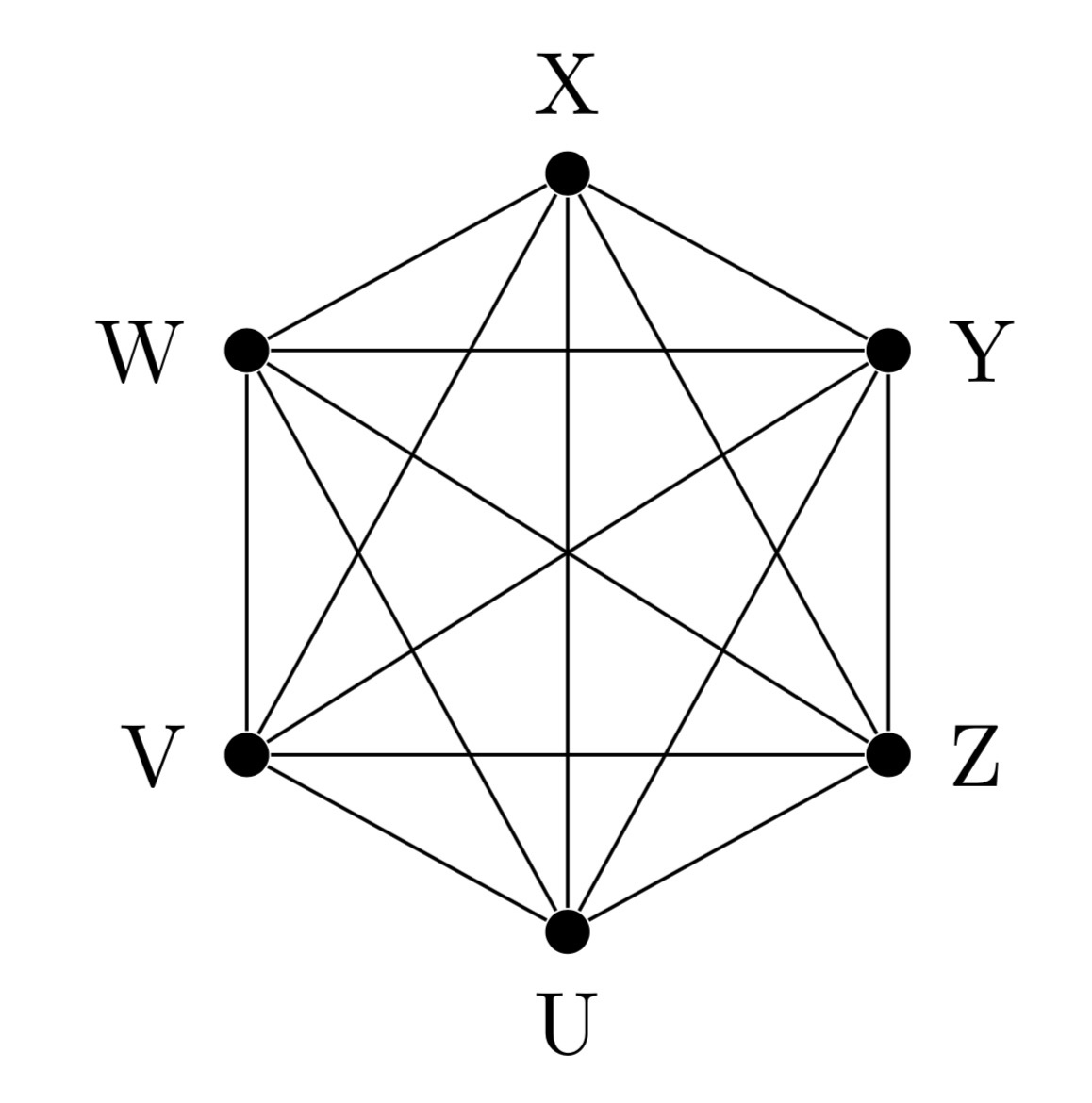
estimating causal effects will be nearly impossible. Besides the fact that the graph is obviously not acyclic, if all variables in the model are causally related, you would need to observe all of them at just the right frequency to get anywhere with identification.

Does that ultimately undermine the usefulness of graphical approaches? Well, I wouldn’t say so. If anything, it shows you how under-speciefied the implicit models we usually work with in the currently prevalent potential outcome (PO) framework are. Because if you really believe that “everything causes everything”, then good luck with justifying your unconfoundedness assumption or exclusion restriction. PO and DAG folks sit – as they say – in exactly the same boat here.

DAGs have one big advantage over PO though. Namely that they disclose crucial identifying assumptions very transparently. In PO, by contrast, you only have an implicit model of the specific context you’re studying in mind. This gives you no guidance whatsoever on how to justify the conditional independence assumptions involving counterfactuals that PO techniques rely on. Whether you’re allowed to call your estimates “causal” is then solely decided by the gut feeling of your seminar attendants and reviewers. As long as they have a hunch that “your treatment is still endogenous” there’s not much you can do – apart from resorting to an argument by authority, maybe.

DAGs have yet another advantage to offer to the the ambitious empiricist. Every graph that you specify gives rise to testable implications, due to the d-separation relationships between the variables in your model. That way it actually becomes possible to check whether the graph is consistent with the joint distribution of the data, which will lend further credibility to your analysis.

If we want to bring DAG methodology forward and achieve a wider diffusion in the community, we clearly need to develop best-practice standards for model building.* And it’s quite evident that models will need to be sufficiently sparse (unless you want to go back to the huge general equilibrium models of the 70s with ten thousand and more equations). In other words, we’ll need to apply a fine Occam’s razor.

I actually expect some kind of convergence with established approaches in economic theory and “structural econometrics” to occur, where the goal is usually to model a couple of key mechanisms in full detail, while leaving the less relevant things “for the error term” in order to keep models tractable.

The good thing is that the testable implications of DAGs always provide the opportunity for an ex-post sanity check. If you realize that the postulated graph doesn’t comply with the data (because some of its d-separation relations are violated), there’s always the possibility to go back to the drawing board and refine the model. Even better, d-separation will guide you exactly to the point where the graph doesn’t fit. So you’re not left in the dark about where to start improving the model, like with other diagnostic tools based on global goodness of fit.

Taking this program seriously also offers a unique opportunity to finally bring back closer together the two competing econometrics camps – PO and “structural”. Making your assumptions explicit – clearly visible for everybody to see in the graph – renders causal inference less of a black box than it currently is under PO. At the same time, you don’t need to be a “structural geek”, who solves systems of equations as a distraction before bedtime, in order to work with graphs and do good empirical work. If you ask me, DAGs offer a perfect middle ground, with just the right balance between complexity and tractability. It’s worth to have a look into them!

---

* There’s no such thing as “model-free causal inference” – in case you were wondering.