Update: The success of this blog post motivated us to formulate our point in a bit more detail in this paper, which is available on arXiv. Check it out if you need a citable version of the argument below.
I’m currently reading this great paper by Carlos Cinelli and Chad Hazlett: “Making Sense of Sensitivity: Extending Omitted Variable Bias”. They develop a full suite of sensitivity analysis tools for the omitted variable problem in linear regression, which everyone interested in causal inference should have a look at. While kind of a side topic, they make an important point on page 6 (footnote 6):
[…] since the researcher’s goal is to estimate the causal effect of D on Y , usually Z is required only to, along with X, block the back-door paths from D to Y (Pearl 2009), or equivalently, make the treatment assignment conditionally ignorable. In this case,
could reflect not only its causal effect on Y , if any, but also other spurious associations not eliminated by standard assumptions.
It’s commonplace in regression analyses to not only interpret the effect of the regressor of interest, D, on an outcome variable, Y, but also to discuss the coefficients of the control variables. Researchers then often use lines such as: “effects of the controls have expected signs”, etc. And it probably happened more than once that authors ran into troubles during peer-review because some regression coefficients where not in line with what reviewers expected.
Cinelli and Hazlett remind us that this is shortsighted, at best, because coefficients of control variables do not necessarily have a structural interpretation. Take the following simple example: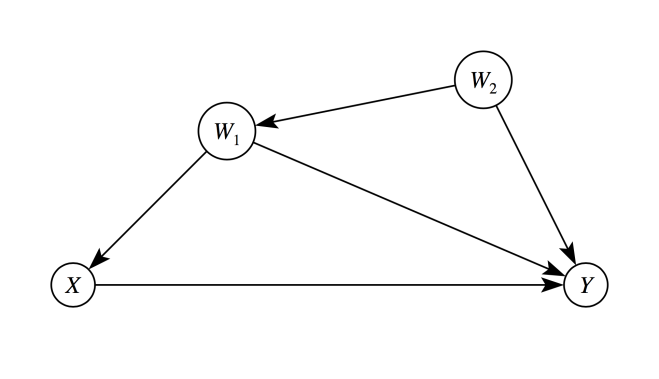 If we’re interested in estimating the causal effect of X on Y, P(Y|do(X)), it’s entirely sufficient to adjust¹ for W1 in this graph. That’s because W1 closes all backdoor paths between X and Y, and thus the causal effect can be identified as:
If we’re interested in estimating the causal effect of X on Y, P(Y|do(X)), it’s entirely sufficient to adjust¹ for W1 in this graph. That’s because W1 closes all backdoor paths between X and Y, and thus the causal effect can be identified as:
However, if we estimate the right-hand side, for example, by linear regression, the coefficient of W1 will not represent its effect on Y. It partly picks up the effect of W2 too, since W1 and W2 are correlated.
If we would also include W2 in the regression, then the coefficients of the control variables could be interpreted structurally and would represent genuine causal effects. But in practice it’s very unlikely that we’ll be able to measure all causal parents of Y. The data collection efforts could just be too huge in a real-world situation.
Luckily, that’s not necessary, however. We only need to make sure that the treatment variable X is unconfounded or conditionally ignorable. And a smaller set of control variables could do the job just fine. But that also implies that the coefficients of controls lose their substantive meaning, because they now represent a complicated weighting of several causal influence factors. Therefore, it doesn’t make much sense to try to put them into context. And if they don’t have expected signs, that’s not a problem.
¹ The term control variable is actually a bit of an outdated terminology, because W1 isn’t controlled in the sense of an intervention. It’s rather adjusted for or conditioned on in terms of taking conditional probabilities. But since the term is so ubiquitous, I’ll use it here too.
Wonderful explanation!
LikeLike
very neat argument, thanks!
about to reveal my ignorance, but I am having a hard time squaring this argument with the simple one made here: https://stats.stackexchange.com/questions/242585/inconsistent-estimators-in-case-of-endogeneity
your argument seems to suggest that a multi OLS can have one consistent beta and a few inconsistent betas, but the argument in the link is clear that this cannot happen except under very non-standard assumptions. am I missing something obvious?
LikeLike
Hi Julian,
This is a great example how standard econometrics textbooks obscure the issue compared to a DAG framework. The argument in Wooldridge isn’t wrong, it’s just hard to see what’s going on. The key here is that there’s a second condition. You end up with all regressors being biased unless x_k is (conditionally) uncorrelated with the omitted variable. In the blog post, w_2 is the omitted variable and w_1 d-separates x from w_2. So you can consistently estimate the effect of x, while the coefficient of w_1 will be biased. See also the simulation in footnote 4 of this paper: https://arxiv.org/abs/2005.10314 In my view, the backdoor criterion makes these things much clearer than thinking about error correlations, as the issue is usually presented in standard econometrics textbooks.
Best,
Paul
LikeLike