This is a fair copy of a recent Twitter thread of mine. I thought it might be interesting to develop my arguments in a bit more detail and preserve them for later use.
Mediation analysis is a ubiquitous tool in social science and business economics.¹ The reasons are clear. For many important policy questions, knowing that a particular effect exists is not enough. You also want to examine the causal mechanism through which an effect comes about.
Take the classic example of the gender wage gap in labor economics. The fact that average wage levels of females are lower than those of males in most (all?) advanced economies is indisputable. But how should we react to this information? The appropriate policy response differs dramatically depending on whether there is either systematic discrimination against females in hiring and promotion decisions, or whether women voluntarily choose to work shorter hours, e.g., to take care of the kids.
To answer this question, we need to conduct a mediation analysis and test how much of a total effect from X (gender) to Y (wage) is transmitted via a causal path going through a third variable M (gender-biased attitudes by superiors).²

This allows us to decompose the total effect into a direct effect (X → Y) and a mediation effect (X → M → Y), and hopefully leads to better targeted policy responses.
Mediation analysis is almost exclusively done and taught within the linear structural equation modeling (LSEM) paradigm, going back to the seminal article by Baron and Kenny (1986). The linear functional form assumption is so omnipresent that standard textbooks, such as Kline (2005), don’t even bother to waste much time on them. For someone like me, with an econometrics background, this is truly amazing—boxes and arrows everywhere, but not one equation throughout the book.
These days, however, there is a newer literature on mediation analysis out there, based on the work by Imai, Tingley, and Keele (and subsequent coauthors). These authors worried about how we can identify causal mechanism in fully general (i.e., non-parametric) models, without assuming linearity. Non-parametric models are, of course, not that useful in practice, because they are usually too data-hungry. Once we have established non-parametric identification though (meaning, we can be sure that we are able to estimate what we want to estimate), it’s easy to re-introduce parametric functional form assumptions. But we’re not bound to linearity. For example, I’m currently working on project in which we use an ordered logit model for the mediator M, and a poisson count data model for the outcome Y.
One important result of the newer mediation literature is that the task of identifying causal mechanisms can be pretty tough, because it relies on strong untestable assumptions. One such assumption, which is necessary in mediation analysis in particular, is sequential ignorability (SI). I won’t go into technical details here, for that you will need to read the respective papers. But SI would be violated, for example, if there is an unobserved confounder between the mediator and the outcome, as illustrated in the following graph.
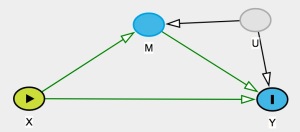
What’s important here is that sequential ignorability is not just an additional complication that we’ll buy in if we move to a more general model. It’s equally necessary in the linear case. The LSEM framework just largely obscures these important ingredients.
SI is particularly problematic if we have more than one mediator in our model. Such a situation is frequent in the social sciences. Discrimination against females in the workplace can manifest itself through many different causal pathways and researchers usually have the ambition to separate as many as possible of them. If mediators are not completely causally independent from each other though (such as in the following graph where there is a causal link from mediator 1 to 2), it can be hard to satisfy SI.

In this particular situation, we would be able to estimate the total effect of X → M1 → Y (going partially through M2 too), but there is nothing you could do to tease out the separate effect of M2. Also invoking linearity won’t help! If mediation analysis is an important tool in your research, or you are interested in more details, I suggest you to read this paper by Kosuke Imai and coauthors, published in the American Political Science Review. It’s a rather easily digestible starting point to delve further into the literature.
Okay, let’s see. This post is already long enough, and I haven’t even made it to my later tweets about theory development. I guess I’ll save that for a second part then.
¹ In economics it’s often not perceived so favorably though.
² Graphs are produced with DAGitty.